From New Dawn 157 (Jul-Aug 2016)
Although it’s been moving more into the spotlight for today’s “New Age” devotees, the basic principles of what is known as Sacred Geometry are still little understood. In this 3-part series of articles, we will attempt to demystify the subject. Let’s begin by defining Sacred Geometry…
Webster’s Dictionary defines sacred as synonymous with holy. Aside from the usual religious connotations, a more general meaning given is: “devoted exclusively to one service or use (as of a person or purpose).” When, years ago, I was involved in church design, we usually planned for a very particular room called the ‘sacristy’. It’s also known as the vestry where the sacred utensils and vestments that are used in liturgical ceremonies are kept.
Sacred has a Latin root the same as that for the word sacrum. The sacrum is the last bone in the spine. Webster says it’s the “holy bone” and consists of “the part of the vertebral column that is directly connected with or forms a part of the pelvis and in man consists of five united vertebrae.” You will see later in this and subsequent articles how the relationship to human anatomy plays directly into our subject matter.
There’s another little-known synonym for sacred, and that is the word secret. Here, it implies something esoteric or meant only for a few to understand about geometry. While that may have been true in the past, I believe it is important at this time in history for more folks to understand the implications of the kind of geometry we call sacred. Indeed, it can be said the earth is sacred as we depend upon it for our very existence.
The word geometry literally means “to measure the earth,” an easy definition. We all know what it is to measure something: its length, breadth, and height. But, if we’re measuring the earth, is it the whole (holy) earth or just a small portion of our globe? Or is there a wider meaning to the word Earth? Is it perhaps more appropriate in our context to use the word ground, as in “hallowed ground?” Many of us sometimes use the verb grounding that has physical and psychological implications. In fact, as we proceed, I think you’ll see that the physical and the psychological begin to merge into each other.
The Language of Numbers & Symbols
The various languages spoken around the world since the beginning of recorded history were not the first means of communication between human beings. Archaeology shows us that early man communicated first by the use of different kinds of symbols. From symbols came numbers, which are in themselves particular kinds of symbols.
We know that in distant antiquity man began using a pictorial mode to communicate, whether it was carving into stone or merely tracing with a stick in sand or on the ground. As we became more sophisticated, sheets of papyrus and later paper made from wood pulp were marked upon. Figures, letters, and numbers were generated with ink or paint by using pen, pencil, brush, or, later, typewriter. Today they are produced with the aid of computers. No matter how they are scribed, numbers and symbols remain a universal language.
Sacred Geometry (let’s call it SG for short) employs both numbers and symbols, but in very specific ways. While similar kinds of graphic representations are used in drawings for constructing a building or in mathematical equations, in SG they are used in a very precise manner. As Webster’s says, they are “devoted exclusively to one service or use….” Symbols in SG have very unique meanings, although, in keeping with our definition of sacred as secret, those meanings are not generally known.
The language of numbers and symbols (we’re talking about pure numbers here, not the process of using numbers to make calculations) is the language of certain human brain faculties that are different from those used to produce and communicate with the spoken word. As we have noted, some say the language of symbols is the more primitive form of communication. But with SG we begin to glimpse a highly sophisticated symbolic language that transcends the spoken or written word.
It has been shown that language is a function of the left hemisphere of the human brain (at least for most right-handed people). So is ordinary mathematical calculation. Symbols, on the other hand, are interpreted by the right side of the brain, as are pictures and other visual images. We all know the phrase, “A picture is worth a thousand words.” In SG, a single shape or form can have very distinctive meanings that would take many pages of written words to explain.
Our first task is to learn the language of Sacred Geometry.
As Above, So Below
Primitive man could see the stars in the night sky, unhindered by the reflection of city lights off clouds and layers of atmosphere. We have discovered that the Egyptians and the Maya, along with numerous other ancient civilisations, were close watchers of the night sky. We are just now finding out they knew things we have only come to know with the advent of the telescope. How they knew as much as they did about the heavens is being investigated by researchers. It remains a mystery, but perhaps not for too much longer.
The most striking example of a representation made by the ancients on earth which reflects something visible in the night sky is the layout of pyramids on the plateau at Giza, across the Nile River from Cairo, Egypt.
Robert Bauval and Adrian Gilbert in their 1994 book The Orion Mystery make a good case that the three Giza pyramids, when viewed from above, form a replica of the position of the three stars in the ‘belt’ of the constellation Orion. In another book by Bauval and Graham Hancock published two years later in 1996, The Message of the Sphinx, the theory is expanded to show that other pyramids in the complex also fit the Orion constellation. As we are now able to calculate star movements over thousands of years with a computer, the position of the stars in the Belt of Orion form a match only at a time well before the Giza pyramids are claimed by Egyptologists to have been built. (More recently, researcher John Anthony West and geologist Robert Schoch have shown that the erosion around the Sphinx was caused by water, not wind. It was at least 10,000 years ago that the desert in northern Africa was a lush and verdant environment with enough rainfall to account for that erosion. If the first or Great Pyramid at Giza was built at about the same time as the Sphinx, the earlier date of the correspondence to the Orion Belt does make sense.)
Since the seminal work of Bauval, Gilbert and Hancock, others have expanded the search and found numerous ancient sites around the world that replicate in some manner what we see in the night sky, or use the sun, planets, and certain bright stars as the basis for orienting their manmade constructions. Stonehenge in southern England is probably the best known example of the latter. But there are hundreds if not thousands more such ruins.
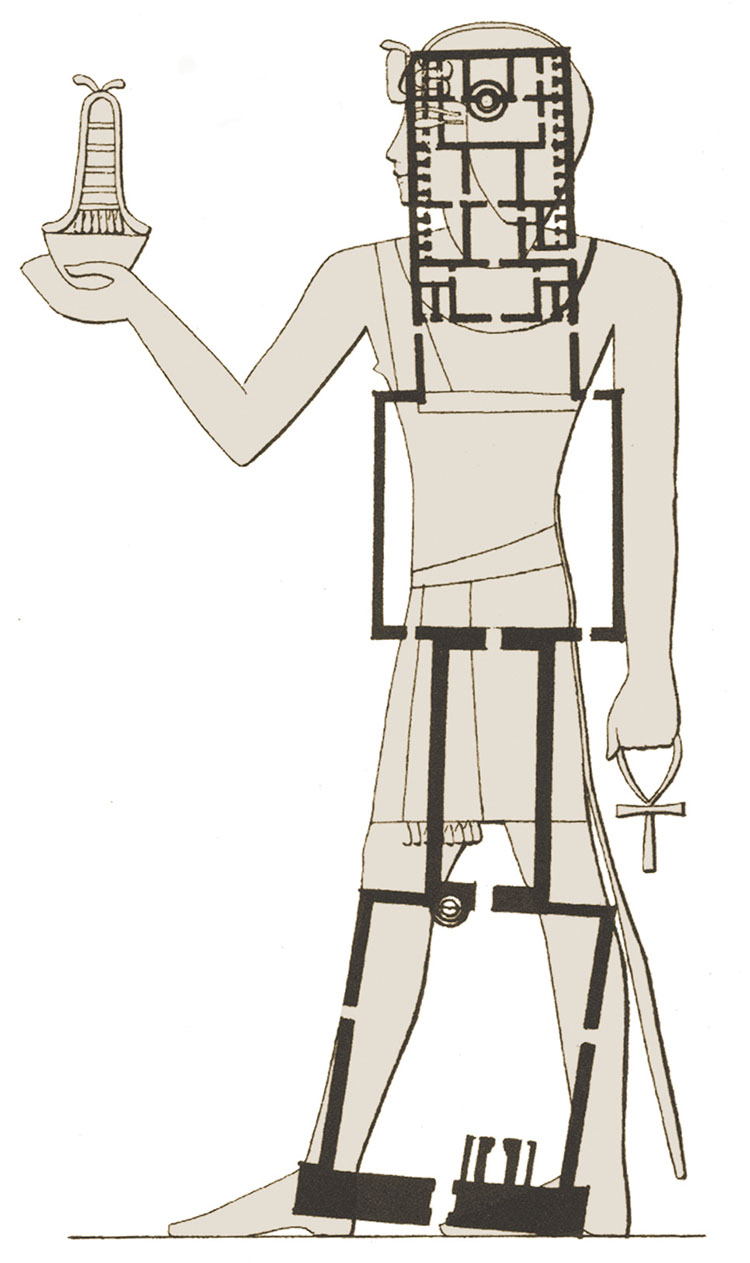
At another scale of measurement, “as below,” we find that certain ancient structures were undoubtedly patterned after the anatomy of the human being. R.A. Schwaller de Lubicz made a 15-year study of the architecture of Egypt’s Luxor Temple. His magnum opus, The Temple of Man, shows how the floor plan of Luxor and its parts mirror the human body. He even goes so far as to identify various chambers in the Temple with parts of the brain.
Builders associated with the Knights Templar encoded images of parts of the human body within the geometry of the great Marian Gothic Cathedrals in France. No mere coincidence as we shall later see. And, “as above,” it has been shown that the overall pattern of placement for those Marian Cathedrals bears a striking resemblance to the configuration of stars in the constellation Virgo, the Virgin.
On the molecular scale, James Watson and Francis Crick published a paper in 1953 in which they identified the structural shape of DNA as a double helix. Recently a double helix-shaped gas nebula was discovered lying nearly perpendicular to the massive black hole at the centre of our Milky Way Galaxy. Also, in what we might call the middle ground of the human measurement scale, we see the double helix represented in architecture, and sacred architecture at that. The “Apprentice Pillar” inside Scotland’s Rosslyn Chapel, made famous by Dan Brown’s Da Vinci Code, illustrates an example on its surface of a double (or even triple or quadruple) helix carved in stone.
All this is in keeping with the ancient saying attributed to Hermes Trismegistus and long the familiar slogan of SG practitioners, “AS ABOVE, SO BELOW.”
Incorporating the Ratio F and the Number 5
The Third Food of Man
In designing buildings for use by human beings we always keep in mind the size and proportions of the human body so our constructions are easily related to human functioning. The dictum of the great 20th century Swiss architect Le Corbusier, “A house is a machine for living,” applies in a broader sense to all construction types and uses. However, what is sometimes forgotten is that human functioning is both external and internal. Yes, the body walks and crawls, stretches and reaches, climbs and descends, sits and lies down. But these are only some of its outward manifestations. We must not forget our internal workings. Not only does a healthy person use all five physical senses, but the body, mind and emotions form impressions from an aggregate intake of those senses. Just as from food and drink we nourish the body, and from the air we breathe we extract oxygen, for our living and being, so do impressions form another kind of food. In fact, without the intake and processing of impressions (even while we’re sleeping), we are considered dead. In spite of artificial respiration and intravenous feeding, a physician still considers a patient clinically dead if there are no brain waves exhibited on the EEG monitor.
Just as fresh food and clean air keeps our body healthy, it can be shown we thrive better with positive impressions. Those who design and build the living environments should strive to produce surroundings the inhabitants perceive as having pleasing proportions, colour, texture, and scale beyond mere operational functionality. Humans have physical bodies that we assess as more attractive or less attractive aesthetically, and it is the same with buildings. Interestingly, we apply many of the same criteria to our perceptions of architecture as we do to judgments on human form. So much so that pleasing and even inspiring architecture can be shown to correlate to specific qualities of the human body. This is undoubtedly why many of the great visual artists have also been great architects.
Measuring Man by the Golden Mean
In order to proceed with this line of study, a good place to begin is with Leonardo da Vinci’s so called ‘Vitruvian Man’.
Leonardo was concerned with seeing the harmony in human anatomy, and this sketch among his many anatomical studies is perhaps the best example. It sets the proper proportions for all subsequent artists and sculptors of the human form. And, as evidence of his wisdom, it also shows us the relationship between anatomy and pure geometry. As the saying goes, “Man is the measure of all things.” Also, in keeping with our guide phrase “As Above, So Below,” we see the parts of the body expressing the same ratios as the whole.
The ancient Egyptians, Greeks, Japanese and even older cultures around the world long ago identified the ratio of the circumference (C) of a circle to its diameter (D) as C/D = 3.14159… Most of us know from high school geometry class that we represent this number by the Greek letter p (Pi). It’s called an ‘irrational’ number as it can be carried out to an infinite number of decimal places depending upon how exact we want to be.
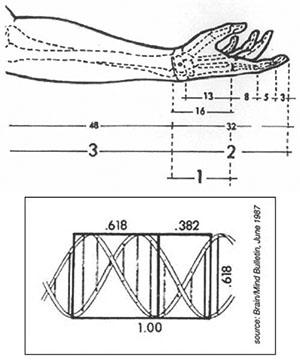
Another important ratio, but one we are usually not taught in high school, is represented by the Greek letter F (Phi), where F = 1.618… (also an ‘irrational’ number). It is derived from what is alternately called the Golden Mean, Golden Proportion, or Golden Section – a relationship that satisfies the classical definition of “a proportion whose whole is to the greater part as the greater part is to the lesser.” For those of us who are graphically inclined, we can see this proportion by drawing a line segment and dividing it into two parts, a and b, with the ratio of 1:F as shown below:
a = 1 b = F = 1.6180339887…
In algebraic terms, it is represented by the equation: (a + b)/b = b/a. This relationship can only occur if b/a = 1.618…, the numeric value of F. We can easily see this if we assign a value of 1 to a and 1.618… to b. Take a pocket calculator and do the simple math yourself. The more decimal places you include, the closer you will approach the value of F.

The ancients used this Golden Mean proportion in designing their buildings. The Parthenon in Athens and the Great Pyramid at Giza immediately come to mind. Aside from the numerical value itself and ignoring for a moment that this ratio is supposed to represent an ideally pleasing proportion (so we’ve been told), what is its relationship to man/woman in general and, specifically, to Leonardo’s sketch of the Vitruvian Man?
Five, the Number of Man
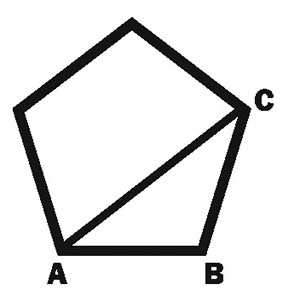
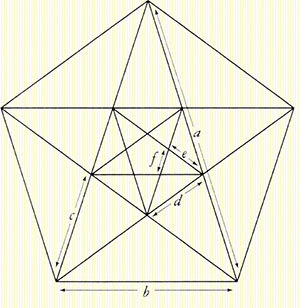
Without getting into any more calculations at this point, let me say that the number 5 plays a significant role in the Golden Mean. To easily illustrate this, let’s generate a regular 5-sided figure, a pentagon, with each side measuring one unit as shown here
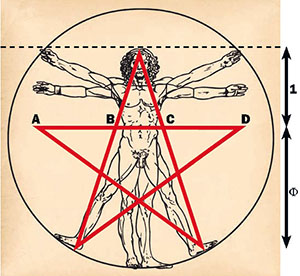
so that AB = BC = 1. Now, if we connect any two opposite points with a straight line (for instance, AC), that line will measure 1.618…, the numerical value of F. Of course, if we look at man/woman in frontal outline form, we see five appendages extending from the central body trunk: two arms, two legs and a head. If we take Leonardo’s Man and slightly rotate the position of the arms downward, we can superscribe a perfect pentagon around the figure. Within that pentagon we can inscribe a perfect pentagram – a five-pointed star, as shown below in a sketch attributed to Agrippa. It goes without saying that both the pentagon and the five-pointed star have great significance, especially in the United States.
We have in “five-foldness” a number and geometric shapes with profound and multi-layered meaning. Man himself and woman herself are symbolically represented overall by that number and by those shapes. And, once more, “As Above, So Below” applies: we have five fingers on each hand and five toes on each foot. The whole is echoed in the parts. And that’s just the beginning.
Above is an overlay drawing (not to scale). If we assign a value of 1 to the distance from the line AD measured vertically to the top of the man’s head, then, measuring vertically downward from AD to the bottom two points of the pentagram at the man’s toes, we find that distance is 1.618… Also, we find the following ratios: AD / AC = F , and AC / AB = F. Again, the parts are in proportion to the whole.
Centre of Gravity
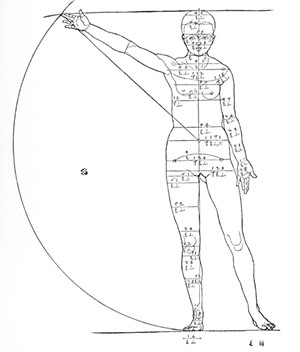
Finally, we have Albrecht Dürer’s sketch showing the human body divided by F at the navel and divided in half by the sex organs:
When a baby is born, the navel divides the body in half. As the child grows up, the bodily proportions change so that the legs are longer in relation to the trunk. By adulthood, the navel has moved up (relative to the person’s total height) to the position of the F ratio as shown in both the da Vinci and Dürer drawings. Some say this represents the principle of a human being maturing from a nature of duality to a nature of asymmetrical but harmonious proportionality. It is interesting to note that the level of the navel is seen in some Eastern traditions as a person’s Centre of Gravity and is used as such in certain meditative practices.
Nature Displays Phi, Fibonacci, & Five
Leonardo Bigollo Fibonacci, also known as Leonard da Piza (Pisano), travelled to Algiers as a young man and brought back to Europe the use of Arabic numerals to replace the cumbersome Roman numeral system. From geometers in Algiers he also learned about various additive series of numbers which are generated by the Golden Ratio of phi.

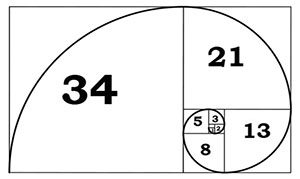
There are many sequences of whole numbers that are called additive series (progressive numbers that are generated by adding the first and second numbers to arrive at the third number), but only one such sequence is classified by what is now known as the Fibonacci Series: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, and so on. The interesting thing is that when we calculate the ratio between each number and the one just before it in the series, the higher we go the closer we arrive at the numeric value of phi. For instance, 5/3 = 1.666666…; 55/34 = 1.617647; and 987/610 = 1.6180327.
Fibonacci Series Logarithmic Spirals
From the Fibonacci succession of numbers we can geometrically produce a particular kind of spiral. One way to do this is by nesting ever increasing sizes of 90 degree rotated rectangles divided with squares according to the phi ratio, and then connecting the points where the squares divide the sides of the rectangles into Golden Ratios with curved lines that trace one-quarter of a circle. The resultant areas of the squares are in the sequence of the Fibonacci Series of numbers, as shown below:
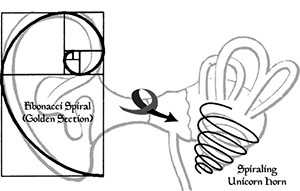
It just so happens that we see such a Fibonacci Spiral repeated time and time again in Nature. In fact, while symmetry is often seen in our world (for example, we have two symmetrically placed arms, legs, eyes, ears, nostrils, etc.), there are actually more examples of the asymmetry of the Fibonacci Series. The problem is that we’ve forgotten to look for them.
The Fibonacci Series is represented in the structure of many living organisms and physical processes such as the distribution of leaves on a plant, spiral seashells, flower petals, the bottom pads on the foot of a cat, the planetary orbit of Venus as seen from Earth, the distribution of seeds on a cactus and on a sunflower, changes in the radiation of energy, the ratio of male to female bees in a hive, the DNA molecule, the surface pattern of pine cones, multiple reflections of light through mirrors, the cochlea of the human ear, the breeding pattern of rabbits, spiral galaxies, the path of certain predatory birds flying down to snatch their prey, and much more. Here are pictures of some of these examples:
The Number 5 in Nature
We showed above that the ratio between a diagonal and a side of a regular pentagon equals phi. By connecting all the pentagon’s corners we can inscribe a pentagram star within the pentagon shape. In the figure below, you’ll notice that inside the pentagram is another, smaller pentagon, and within that, too, we can inscribe a still smaller pentagram. This can be done indefinitely going up the scale in size (macrocosm) and down the scale in size (microcosm).
A fascinating characteristic of the lengths of the lines used to make the pentagon/pentagram figure(s) is that, as we proceed from larger to the next smaller line (a to b, b to c, c to d, etc.), the ratio of line lengths to each other is exactly the value of phi.
Visually, this figure begins to resemble a flower. That is to be expected for in Nature we see the number 5 and the subsequent Fibonacci Series played out in many different kinds of flowers. Perhaps the most beautiful is the rose.
All edible fruit-bearing plants have flowers with their number of petals based on 5, while daisies have a number of petals always equal to one of the numbers in the Fibonacci Series.
The internal shape of edible fruit itself is often based upon the number 5 and the Fibonacci Series. For instance, an apple core has 5 seed pod segments that make almost a perfect pentagram.
Inventor Copies Nature’s Efficiency
An article by Kelpie Wilson discussing the annual Bioneers conference in San Raphael, California, highlighted an invention made in the image of the Fibonacci Spiral. Wilson reported:
“Inventor Jay Harman presented a family of designs for fans and impellers based on the natural spirals found in seashells and blossoms. My favorite was a mixer for giant municipal water tanks. When water is stored for long periods, it can stagnate and become unhealthy. Harman’s mixer is tiny, barely bigger than my fist. Turning in the middle of the tank, nothing much happens at first, but over time it sets up a natural vortex in the tank that keeps the water circulating and fresh. Harman said even if you stop the mixer, the vortex will keep on spinning for days.”
Part 2 of this series investigates the Pythagorean Theorem, the Pythagorean properties of numbers 7 & 8, and the Law of Octaves, and appears in New Dawn 158.
Recommended reading
Graham Hancock & Santha Faiia, Heaven’s Mirror: Quest for the Lost Civilization, Crown Publishers, Inc., 1998
Le Corbusier, Le Modulor and Modulor 2 [English edition], Birkhäuser, 2004
D’Arcy Wentworth Thompson, On Growth and Form, Cambridge University Press, 1992
© New Dawn Magazine and the respective author.
For our reproduction notice, click here.